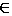 T if U1,U2,...,Un
T if U1,U2,...,Un
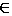 T
T
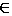 T if U1,U2,...,Un
T if U1,U2,...,Un
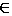 T
T
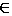 T if U
T if U 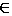 T
T
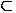 T where A is the set of
atomic values in Prolog
T where A is the set of
atomic values in Prolog
CEng 242 Homework 6
Due: 29th May 2000 (sharp)
You are given a set of terms T with the following recursive definition:
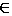 T if U1,U2,...,Un
T if U1,U2,...,Un
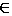 T
T
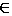 T if U1,U2,...,Un
T if U1,U2,...,Un
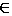 T
T
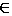 T if U
T if U 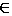 T
T
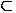 T where A is the set of
atomic values in Prolog
T where A is the set of
atomic values in Prolog
Implement a prolog predicate surface(T,L) where L is a list of atoms representing a valid surface ordering of term T. Valid surface ordering of a term is defined as follows:
 valid orderings
of U
valid orderings
of U
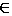 A :
[a]
A :
[a]
See the following examples:
| ?- surface([a,{b,[c,d]},e],L).
L = [a,b,c,d,e] ? ;
L = [a,c,d,b,e] ? ;
no
/****** {b,[c,d]} permuted, [c,d] order is preserved *******/
|?- surface({a,[b,c],d},L).
L = [a,b,c,d] ? ;
L = [b,c,a,d] ? ;
L = [b,c,d,a] ? ;
L = [a,d,b,c] ? ;
L = [d,a,b,c] ? ;
L = [d,b,c,a] ? ;
no
/******* {a, [b,c], d} is permuted (3!), [b,c] is preserved *******/
| ?- surface({{a,b},[c,d]},L).
L = [a,b,c,d] ? ;
L = [b,a,c,d] ? ;
L = [c,d,a,b] ? ;
L = [c,d,b,a] ? ;
no
/****** {a,b} , [c,d] permuted (2!) {a,b} permuted inside (2!) ******/
| ?- surface([opt({a,b}),opt(c)],L).
L = [] ? ; /* Both optionals ommited */
L = [c] ? ; /* {a,b} ommited */
L = [a,b] ? ; /* c ommited p.1 */
L = [b,a] ? ; /* c ommited p.2 */
L = [a,b,c] ? ; /* all counted p.1 */
L = [b,a,c] ? ; /* all counted p.2 */
no
| ?- surface([opt(a),b,opt({c,opt([1,2,3])}),d],L).
L = [b,d] ? ; /* a ommited {...} ommited */
L = [b,c,d] ? ; /* a ommited [1,2,3] ommited */
L = [b,c,1,2,3,d] ? ; /* a ommited */
L = [b,1,2,3,c,d] ? ; /* a ommited */
L = [a,b,d] ? ; /* {...} ommited */
L = [a,b,c,d] ? ; /* [1,2,3] ommited */
L = [a,b,c,1,2,3,d] ? ; /* all counted */
L = [a,b,1,2,3,c,d] ? ; /* all counted */
no
To use {...} syntax in prolog, use the following code to convert {a,b,c,...} to set([a,b,c,...]) which is easier to match in predicates. For example goal toset({1,2,3,4,5},X) will instantiate X as set([1,2,3,4,5]):
toset({},set([])).
toset({X},set(Res)) :- settolist({X},Res).
settolist({X,R},[X|Res]) :- settolist({R},Res),!.
settolist({X},[X]).
Your predicate should not produce duplicate solutions and be smart in processing. Producing all solutions and eliminating duplicates is not allowed. As a hint, taking all permutations in {...} then processing will cause redundancy if there are some optional terms inside. You'd better first process optionals, then generate permutations.