
Fig. 3.1.1
/* program P clause # */ p(a). /* #1 */ p(X) :- q(X), r(X). /* #2 */ p(X) :- u(X). /* #3 */ q(X) :- s(X). /* #4 */
r(a). /* #5 */ r(b). /* #6 */
s(a). /* #7 */ s(b). /* #8 */ s(c). /* #9 */ u(d). /* #10 */
Exercise 3.1.1 Draw program clause trees for p(a), p(b), p(c) and p(d). Which of these have program clause trees all of whose leaves are true (or empty), that is, which of p(a), p(b), p(c), and p(d) are consequences of the program P? See the discussion of program clause trees in section 2.1.
Exercise 3.1.2 Load program P into prolog, turn on the trace, and record what happens for the goal ?-p(X). When an answer is reported, hit (or enter) ';' so that Prolog will continue to trace and find all of the answers.
The following diagram shows a complete Prolog derivation tree for the goal ?-p(X). The edges in the derivation tree are labeled with the clause number in the source file for program P that was used to replace a goal by a subgoal.

The trace (Exercise 3.1.2 above) of the goal ?-p(X) corresponds to a depth-first traversal of this derivation tree. Each node in the Prolog derivation tree was, at the appropriate point in the search, the current goal. Each node in the derivation tree is a sequence of subgoals. The edges directly below a node in this derivation tree correspond to the choices available for replacing a selected subgoal. The current side clause, whose number labels the arc in the derivation tree, is tried in the following way: If the leftmost current subgoal (shown as g1 in the little diagram below) unifies with the head of the side clause (shown as h in the diagram), then that leftmost current subgoal is replaced by the body of the side clause (shown as b1,b2,...,bn in the diagram). Pictorially, we could show this as follows:
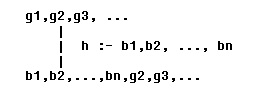
One important thing not shown explicitly in the diagram is that the logical variables in the resulting goal b1,b2,...,bn,g2,g3,... have been bound as a result of the unification, and Prolog needs to keep track of these unifying substitutions as the derivation tree grows down any branch.
Now, a depth first traversal of such a derivation tree means that alternate choices will be attempted as soon as the search returns back up the tree to the point where the alternate choice is available. This process is called backtracking.
Of course, if the tail of the rule is empty, then the leftmost subgoal is effectively erased. If all the subgoals can eventually be erased down a path in the derivation tree, then an answer has been found (or a 'yes' answer computed). At this point the bindings for the variables can be used to give an answer to the original query.
Chapter 8 on Logic Programming Theory has an introduction to the mathematical theory underpinning Prolog.